第一部分
已知某股票当前价格为100美元,股票波动率为25%,无风险利率为5%。考虑以该股票为标的的资产的期权。
无股息
假设股票在期权有效期内不支付股息,取步数为500,1000,1500,2000,利用二叉树模型对有效期为半年、执行价格为100美元的欧式和美式看涨、看跌期权定价,并针对数值结果进行合理的分析。
看涨期权则是估计这个股票会涨,可以在未来以一定的价格买进;看跌期权是估计股价会跌,可以在未来以一定价格卖出。
美式期权(American options)是指允许期权的持有人在期权的有效期的到期日之前任何一天均可履行合约的期权;欧式期权(European options)是指仅允许期权的持有人在期权的有效期最后一天方可履行合约的期权。
以欧式看涨期权为例:
1 | function y = btm_EurCall(S0, K, vol, r, T, N) |
首先我们先进行参数设定:
1 | S0 = 100; % 股票初始价格 |
以下是二叉树模型在不同步数设置下(100:100:2000)给出的数值结果:
欧式看涨期权定价
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15eurcall = [];
for i = 1:length(N)
call = btm_EurCall(S0, K, vol, r, T, N(i));
eurcall = [eurcall, call];
end
[blscall, blsput] = blsprice(S0, K, r, T, vol);
plot(N, eurcall, '*')
hold on
hline = refline([0 blscall]);
hline.Color = 'r';
ylim([8.242, blscall+0.002])
xlabel('steps')
ylabel('European Call Option Price')
legend({'Erucall','blsprice'}, 'Location', 'SouthEast')
hold off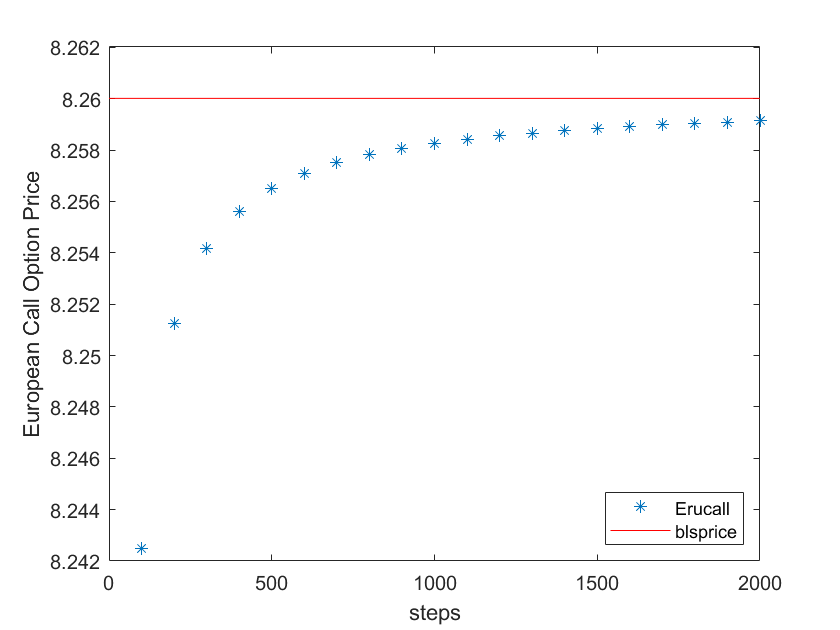
图中所示红线为
Black Scholes所计算的期权价格,可以看到随着步数的增加,欧式看涨期权的价格逐渐逼近blsprice。欧式看跌期权定价
类似上述的代码,我们可以得到不同步数设置下由二叉树模型所得的期权价格
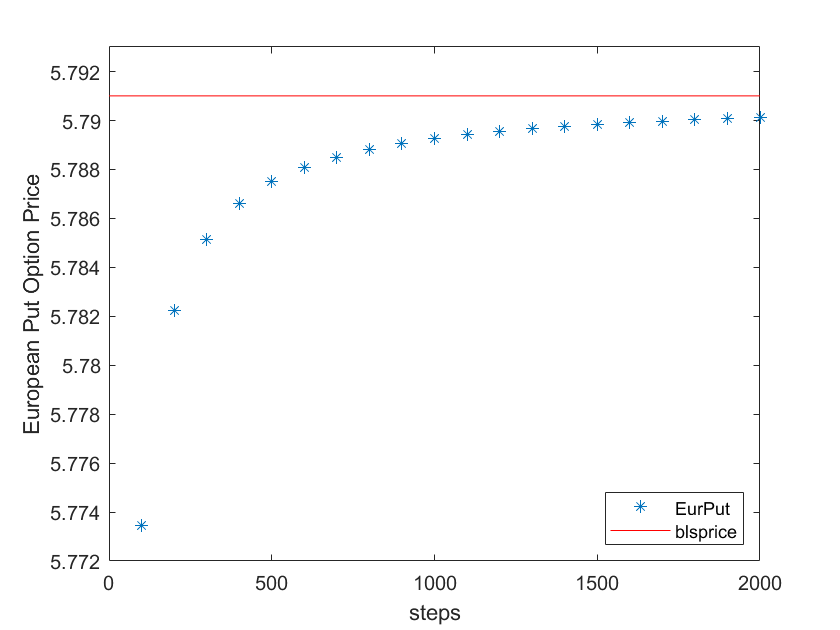
同样的,红线所示为
Black Scholes所计算出的期权价格,我们的数值结果随着步数的增加同样在不断逼近该价格。结合第一点欧式看涨期权我们可以直观的看到欧式看涨期权的价格更贵。美式看涨期权定价
1
2
3
4
5
6
7
8amcall = [];
for i = 1:length(N)
call = btm_AmCall(S0, K, vol, r, T, N(i));
amcall = [amcall, call];
end
plot(N, amcall, '*')
xlabel('steps')
ylabel('American Call Option Price')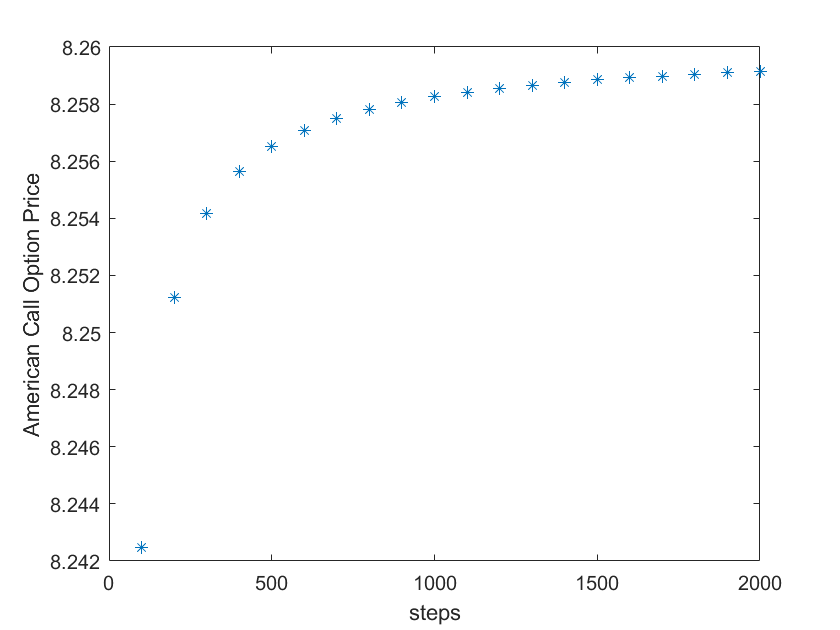
美式看跌期权定价
相应的我们也给出美式看跌期权的数值结果
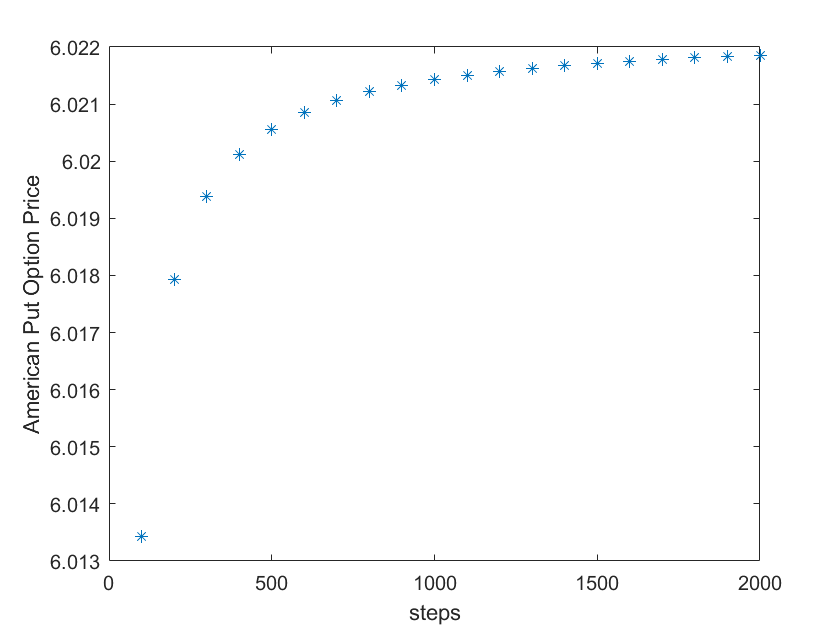
下面我们将美式期权与欧式期权进行横向对比:
欧式看涨期权与美式看涨期权对比
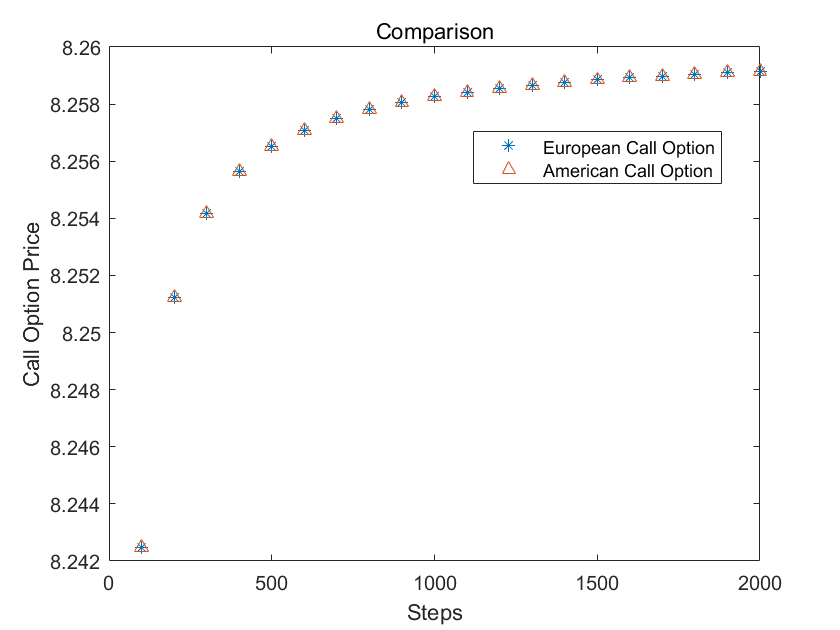
虽然美式看涨期权赋予期权持有人在到期日之前行使期权的权利,理论上美式期权的价格理应更高,但是由于看涨期权持有人在到期日之前行使期权并不能使他获得更多收益,所以在不派发股息的情况下,欧式与美式看涨期权价格并没有区别。
欧式看跌期权与美式看跌期权对比
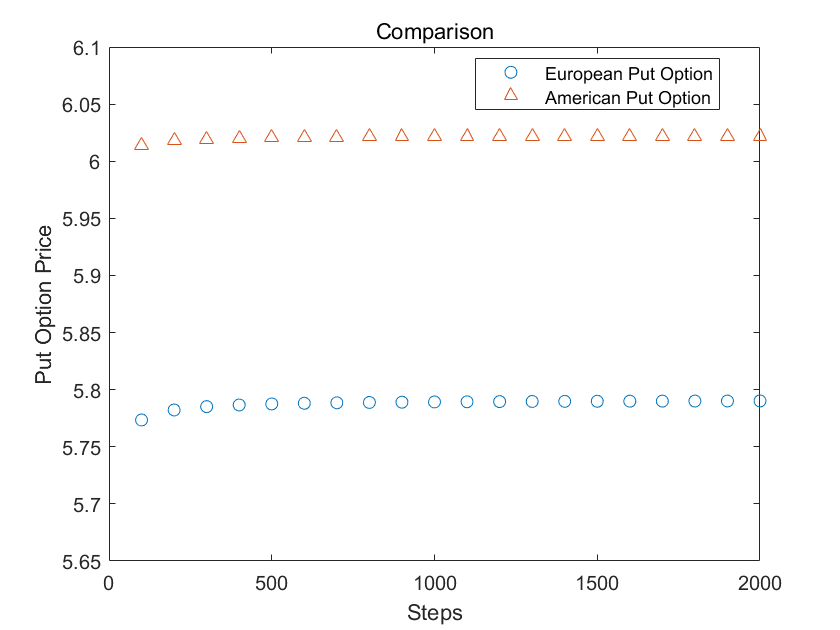
前面说到欧式与美式看涨期权价格在不派发股息的情况下并没有不同,但是对于看跌期权,情况则有所不同,美式看跌期权价格要比欧式看跌期权价格更高。
上升-敲出期权
仍然假设股票不支付股息,取步数为500,100,1500,200,利用二叉树模型对有效期为半年、执行价格为100美元的欧式和美式上升-敲出期权的价格,并针对结果给出金融解释。
鲨鱼鳍期权又称为敲出期权(knock-out options),属于障碍期权(barrier options)的一种。期权合约会事先设置好标的资产的价格区间,如果在合约约定的时间范围内,标的资产价格始终处于该区间中,这个期权就是一个普通的看涨或看跌期权;一旦标的资产价格跳出了该区间,该期权将自动敲出作废。鲨鱼鳍期权作为一种路径依赖的期权,限定了投资者可获的最大收益,所以相对于香草期权更便宜,对于相信标的资产在未来一段时间内会发生确定方向的变化,但是不会越过障碍价格的投资者非常有吸引力。
下表以上升-敲出看涨期权为例展示了多头方到期日的收益(期权价格不计入其中)
| 上升-敲出看涨期权的到期收益 | 标的资产到期价格 | 看涨期权多头到期日收益 |
|---|---|---|
| 标的资产在合约期间不超过障碍价格 | $S_T>=K$ | 0 |
| $S_T>K$ | $S_T-K$ | |
| 标的资产在合约期间超过了障碍价格 | $S_T>=K$ | 0 |
| $S_T>K$ | 0 |
注意到对于一般的路径有关期权,我们并不能直接通过二叉树模型对期权进行定价,因为期权在到期日的收益依赖于股票价格路径,树末端节点处的收益并不明确。但是对于上述这种障碍期权,我们仍然可以使用二叉树模型对其进行定价。
以美式上升-敲出期权为例:
1 | function y = btm_AmUpAndOut(S0, K, vol, r, T, N, H) |
我们首先进行参数的设定:假定障碍价格H为140
1 | S0 = 100; % 股票初始价格 |
欧式上升-敲出期权
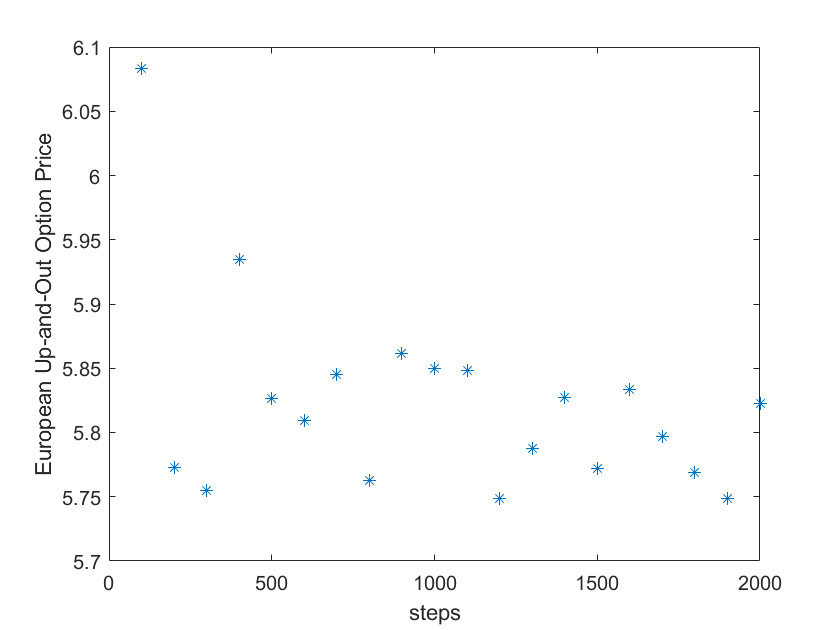
美式上升-敲出期权
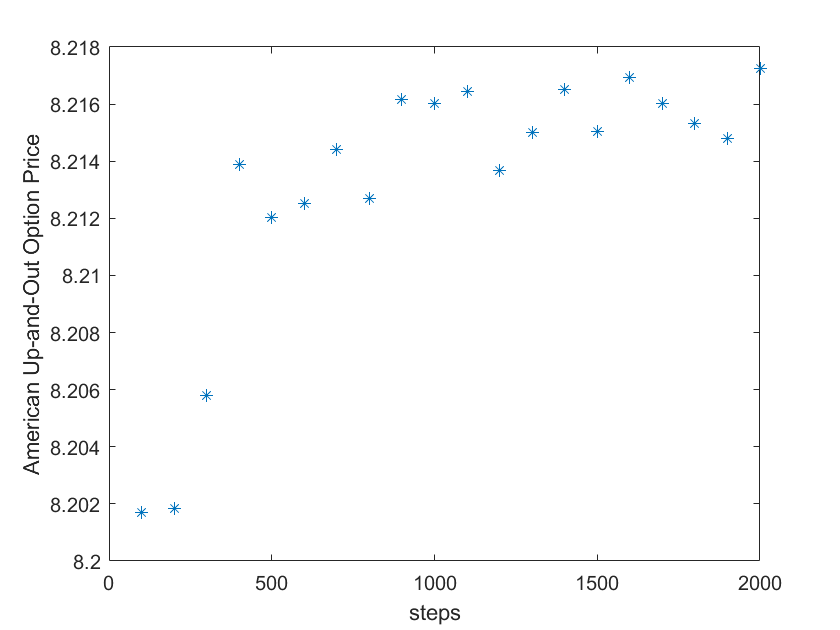
设置步数为2000,我们研究在不同障碍价格设定对欧式、美式上升-敲出期权的影响:
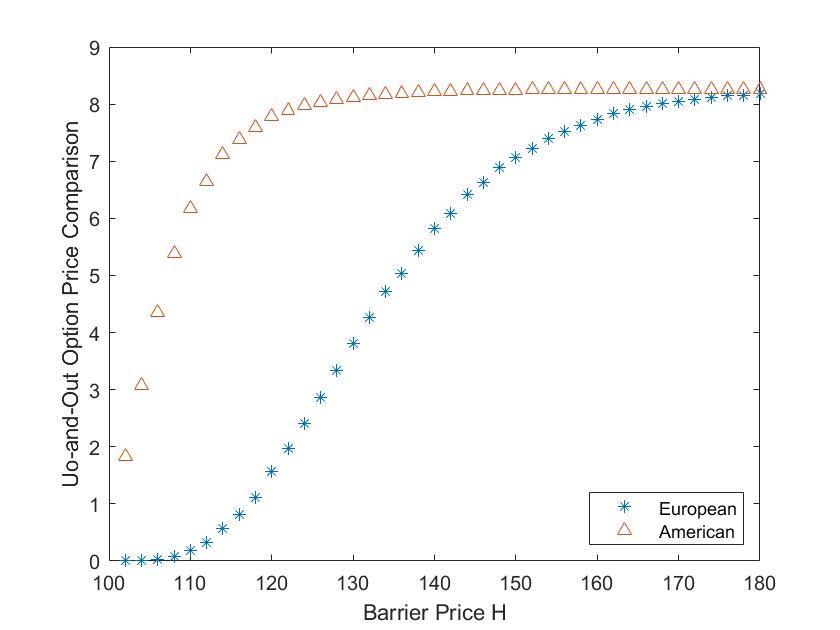
可以看到障碍价格对欧式期权的影响要比美式期权的影响更大。直观上这也很好理解:美式期权赋予期权持有人在到期日之前行使期权的权利,所以当股票价格逼近障碍价格时,美式期权持有人很有可能提前行使期权。
支付连续股息
假设股票支付连续股息,股票收益率为2%,取步数为500,1000,1500,2000,利用二叉树模型对有效期为半年、执行价格为100美元的欧式、美式看涨、看跌期权定价,并针对数值结果进行合理的分析。
假设某股票支付连续收益率为$\ q\ $的股息。在风险中性世界里股息收益率加上资产收益(capital gain)率的总和等于$\ 𝑟$,股息收益率为$\ 𝑞$,因此资本收益率为$\ 𝑟−𝑞$。
资本收益率的变化最终会导致股价上涨概率$\ p\ $的变化
在风险中性世界里,期权的价格等于其未来价格的数学期望以无风险利率$\ r\ $进行贴现
以美式看涨期权为例:
1 | function y = btm_AmCall_ctDiv(S0, K, vol, r, T, N, q) |
首先我们先进行参数设定:设定股票收益率为2%
1 | S0 = 100; % 股票初始价格 |
在呈现支付连续股息的结果时,将同时与无股息情形进行比较
看涨期权
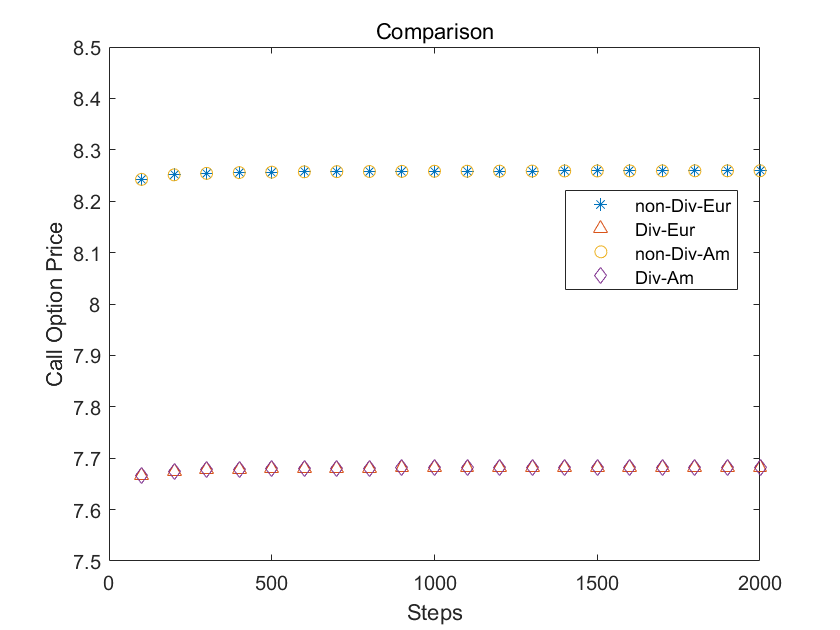
在支付连续股息的情况下,看涨期权的价格下降,这是由于
看跌期权
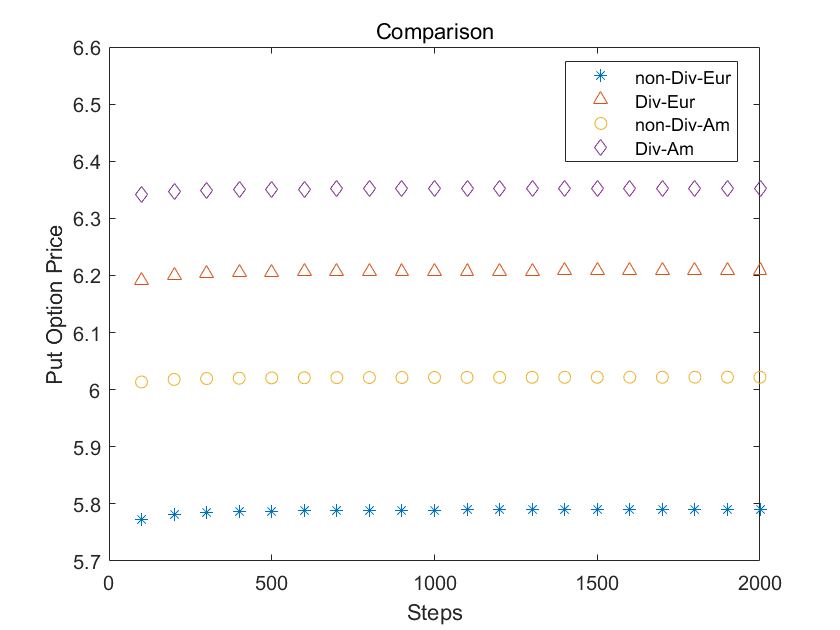
在支付连续股息的情况下,看跌期权价格有所上升。这是因为股息的存在降低了资本收益率,导致股票价格上涨的概率降低,而这对于看跌期权是有益的。
支付一次性股息
假设该股票将于2个月后一次性支付股息,金额为当时股价的2%,取步数为500,1000,1500,2000,利用二叉树模型对有效期为半年、执行价格为100美元的欧式和美式看涨、看跌期权定价,并针对数值结果给出合理的分析。
假定股票只在某个离散时刻点上支付一次股息,而且股息为当时股价的$\ \delta\ $倍,其他参数与没有股息情形下一样。
以美式看跌期权为例:
1 | function y = btm_AmPut_Div(S0, K, vol, r, T, N, delta, date) |
首先我们先进行参数设定:设置一次性股息收益率为当前股票价格的2%,同时假设股息派发时间为2个月之后
1 | S0 = 100; % 股票初始价格 |
下面我们将直接将支付一次性股息的情形与无股息情形进行对比:
欧式看涨期权
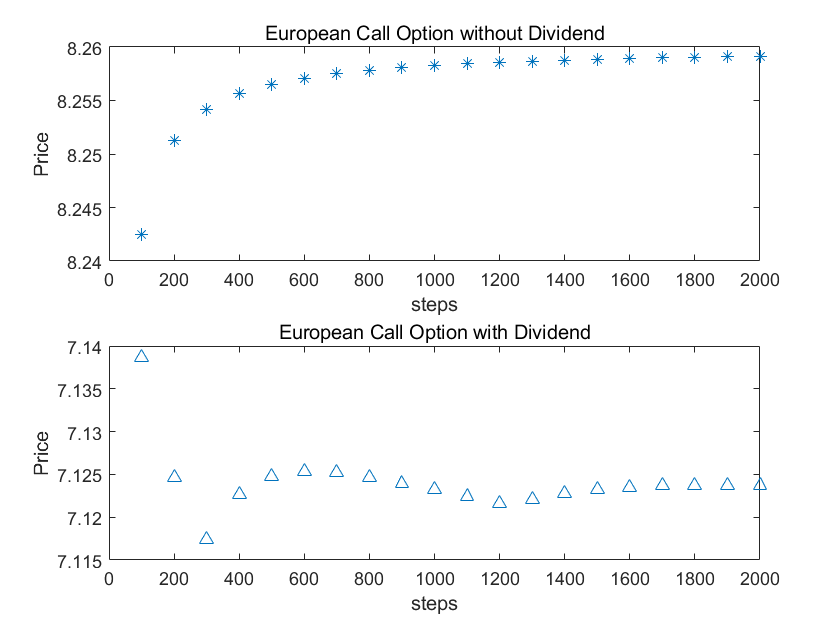
欧式看跌期权
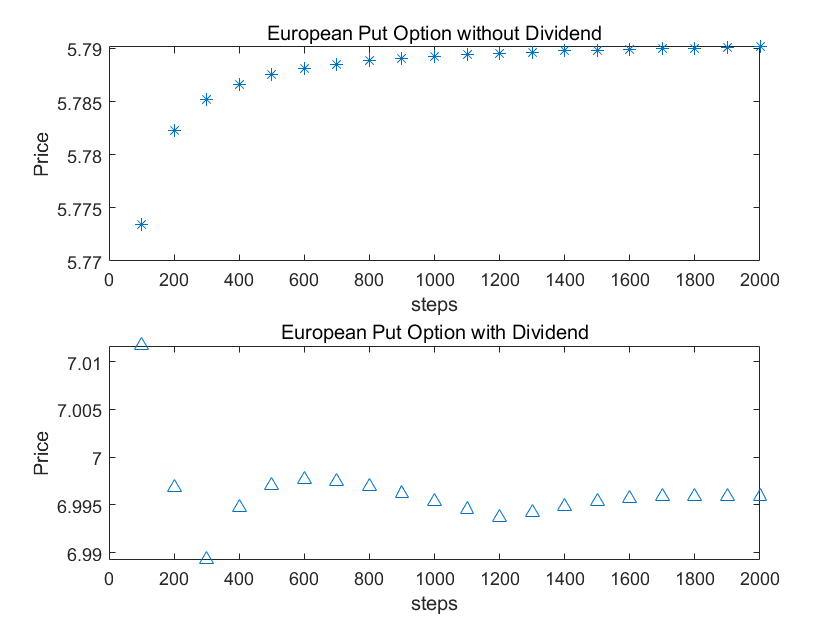
美式看涨期权
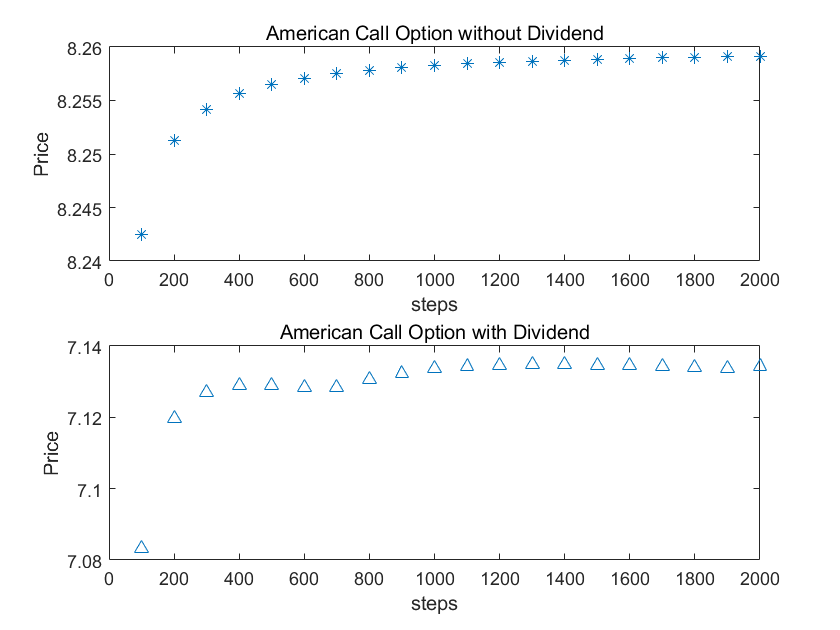
美式看跌期权
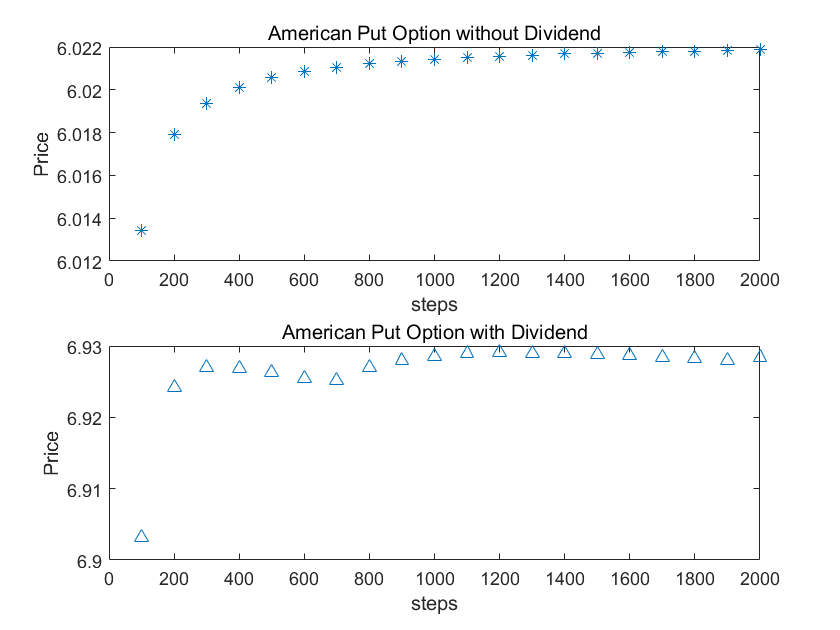
第二部分
已知某股票波动率为25%,无风险利率为5%。考虑以该股票为原生资产的半年期、敲定价格为100美元的欧式看涨、看跌期权。
利用二叉树模型求出初始股票价格为$\ 90:1:110\ $时的欧式看涨、看跌期权的初始价格,并计算出相应的Delta值。
假设在二叉树的某个节点上,股票价格和期权价格分别为$\ S_i\ $和$\ f_i\ $,下一步股票价格可能上涨到$\ uS_i\ $或者降为$\ dS_i\ $,相应的期权价格变成$\ f_{i,u}\ $或者$\ f_{i,d}\ $。
由无套利定价方法,我们知道看涨期权出售方可持有$\Delta = \frac{f_{i,u}-f_{i,d}}{uS_i-dS_i}\ $单位股票对冲掉卖出一份看涨期权所带来的风险。
由于每一个节点所计算出来的$\ \Delta\ $值不同,所以我们在利用股票和期权进行风险对冲时,我们需要不断调整所持股票的数量。
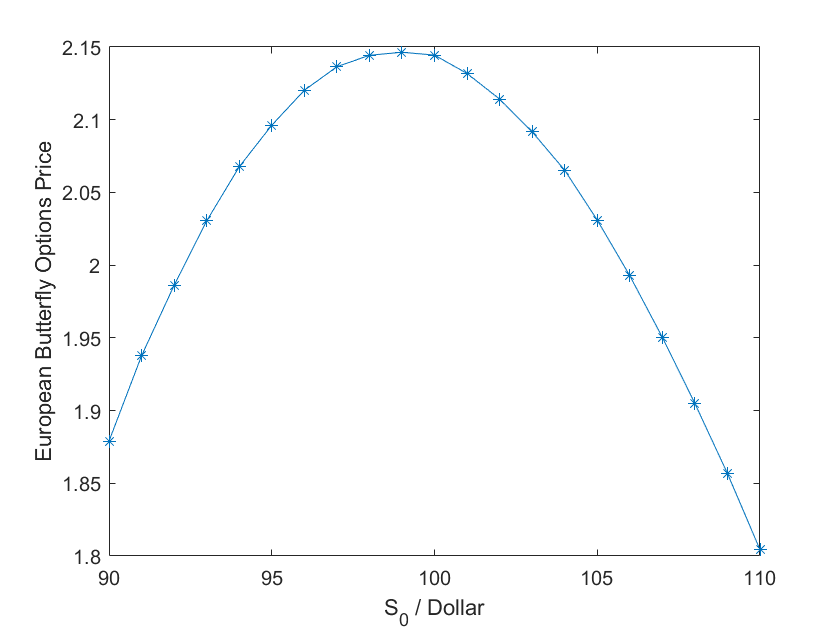
已知蝶式期权时一种欧式期权,它在到期日的收益等于
利用二叉树模型求出初始股票价格为$\ 90:1:110\ $时的蝶式期权的初始价格,并计算出相应点的Delta值。
1 | function y = btm_EurButterfly(S0, vol, r, T, N) |
参数设定:设置股票价格为90:1:110
1 | S0 = 90:1:110; % 股票初始价格 |
1 | for i = 1:length(S0) |