贝叶斯统计漫谈 2

Stein 效应

写在前面

正态均值用其样本均值去估计有很好的性质。人们都经常使用它，当把这样的估计推广到p元正态分布场合时出现了意想不到的结果。Stein在1955年指出，在多元二次损失函数下，$p\ge3\ $时，样本均值向量是正态均值向量的非容许估计。如今，我们把这种效应称为Stein效应。

一致最小方差无偏估计 UMVUE

当我们谈及对某个参数的点估计问题时，我们当然可以根据样本构造很多的统计量，不论它们到底合理与否。不过我们总是希望这些估计量会满足一些比较好的性质，例如无偏性（没有系统性偏差）、相合性（随着样本量的增加可以在概率意义下逼近参数真值）等等。

不仅如此，我们往往还会更加关心是否能够找到一种最优的估计——这种最优性会在一定的框架或者说准则下导出。一致最小方差无偏估计UMVUE（Uniformly Minimum-Variance Unbiased Estimator）就是一个对于所有无偏估计中，拥有最小方差的无偏估计。

容许性

不必回忆干巴巴的数学符号，我们仅通过简单的语言来描述什么是（非）容许估计。

非容许估计就是指在某种准则（决策函数）下，无论参数真值取什么值，某个估计都会一致地比另外一个估计表现差。需要注意两点：一是“一致”是对参数真值而言的，二是表现差是针对具体的准则（决策函数）而言的，换了不同的准则（决策函数），我们的结果可能就截然不同了。

所以很自然地，在一个事先固定的框架下，当某个估计量一致地比另一个估计量的表现差，那么我们就没有任何理由保留前者，此时我们就称它是非容许的。

Stein效应

在有些情况下，如果决策函数选取平方损失函数，可以很容易构造一个比UMVUE一致更优的估计。这一结果最早由统计学家Stein在1955年指出，被称为Stein效应。

例子

考虑p元正态总体均值的估计问题

设$\ \mathbf{x}=(x_1,…,x_p)’\ $服从p元正态分布$\ N(\mu,I_p)$，其中$\ \mu=(\mu_1,…,\mu_p)\in\mathbb{R}^p$，$I_p\ $为p阶单位阵。如今对$\ \mathbf{x}\ $仅作一次观测，并用观测结果

$\delta(\mathbf{x})=(x_1,..,x_p)'$

去估计总体均值向量$\ \mu$，现在决策函数为p元二次损失函数

$L(\mu,\delta)=(\delta-\mu)^T(\delta-\mu)$

下研究$\ \delta(\mathbf{x})\ $容许性问题，Stein在1955年指出$\ \delta(\mathbf{x})\ $在$\ p\ge3\ $时是$\ \mu\ $的非容许估计。1961年，James和Stein给出了比$\ \delta(\mathbf{x})\ $一致更优的估计

$\delta^{JS}(\mathbf{x})=(1-\frac{p-2}{\mathbf{x}^T\mathbf{x}})\mathbf{x}$

这个估计被称为James-Stein估计，选用这个估计的直观想法出自于

$E(\mathbf{x}^T\mathbf{x})=E(x_1^2+...+x_p^2)=p+\mu^T\mu$

这就告诉我们，当用$\ \mathbf{x}\ $去估计$\ \mu\ $时，$\mathbf{x}\ $的平均长度$\ E(\mathbf{x}^T\mathbf{x})\ $实际上比$\ \mu\ $的长度长，这是一种系统性偏差，需要改进，改进的方法就是乘以一个小于1的修正因子使估计量向零收缩。

图示

下图很好地说明了Stein估计与均值估计的差别

图中右侧的文字如下：

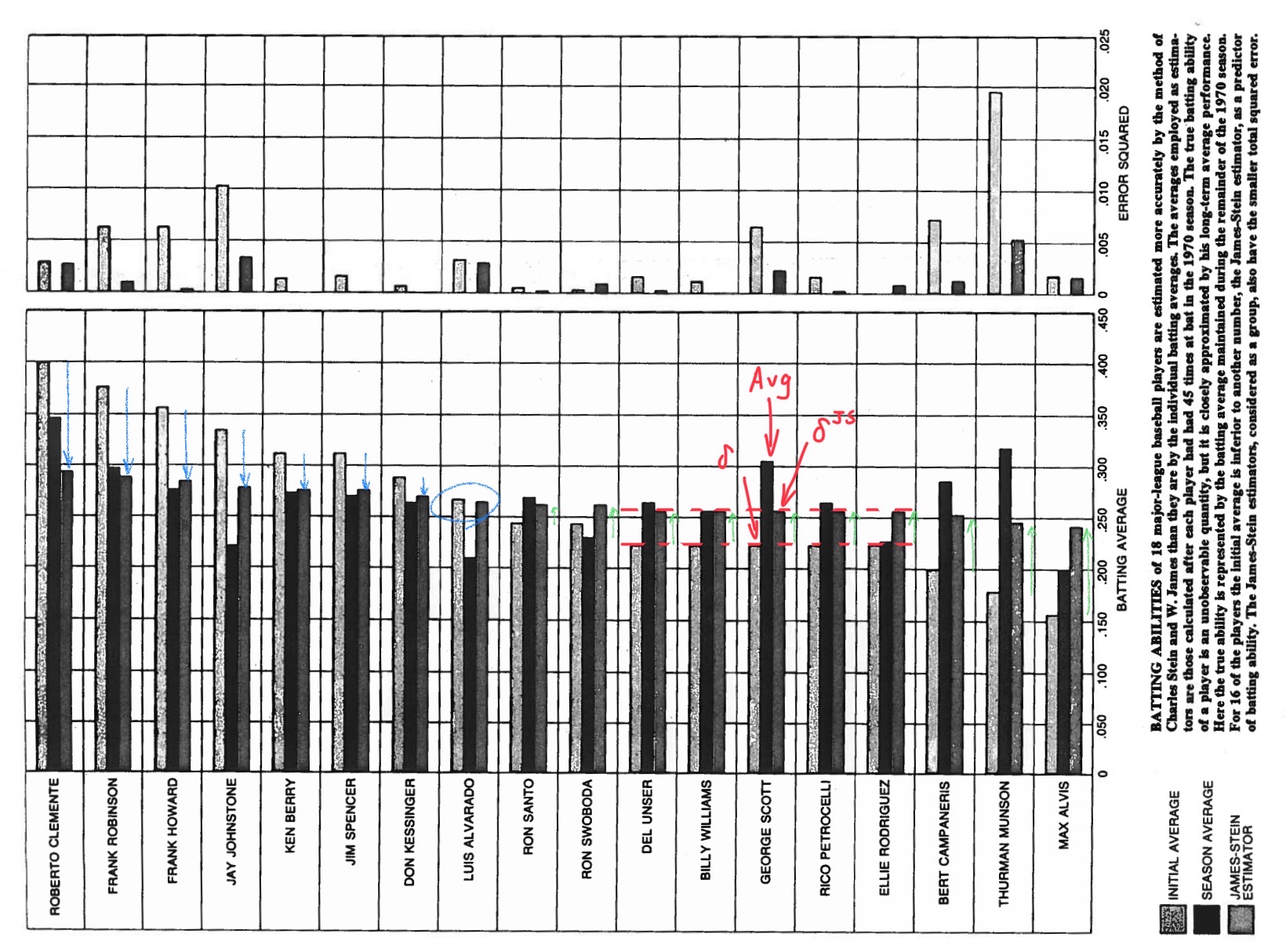
BATTING ABILITIES of 18 major-league baseball players are estimated more accurately by the method of Charles Stein and W.James than they are by the individual batting averages. The average employed as estimators are those calculated after each player had had 45 times at bat in the 1970 season. The true batting ability of a player is an unobservable quantity, but it is closely approximated by his long-term average performance. Here the true ability is represented by the batting average maintained during the remainder of the 1970 season. For 16 of the players the initial average is inferior to another number, the James-Stein estimator, as a predictor of batting ability. The James-Stein estimators, considered as a group, also have the smaller total squared error.

18 名大联盟棒球运动员的击球能力通过查尔斯斯坦和 W.詹姆斯的方法比通过个人击球平均值更准确地估计。平均值估计是在 1970 赛季每位球员击球 45 次之后计算的。一个球员真正的击球能力是一个不可观察的数量，但它与他的长期平均表现非常接近。在这里，由在 1970 赛季剩余时间内保持的击球率代表运动员真正的能力。对于 16 名球员来说，作为击球能力预测指标的初始平均值低于另一个数字 James-Stein 估计值。作为一个组考虑的 James-Stein 估计量也具有较小的总平方误差。

注意看到图表中有18个数据，分别对应18位运动员。每一个运动员又对应着三条柱形：左边柱子表示最初平均值；中间表示赛季平均值，它比较好的逼近了运动员的真实水平；最后一条表示Jame-Stein估计的均值。

用$\ y\ $表示运动员的初步平均击球率，$\bar y\ $表示总平均，$z=\bar y+c(y-\bar y)\ $表示James-Stein估计。这里的参数$\ c\ $就是收缩因子，它的值总是小于1的，而越接近1则表示收缩程度越小。

下图则更好地说明了James-Stein估计的收缩性质

其中每一条线对应着一个或多个运动员的击球能力的估计（如果几个运动员的均值相同，则他们有着相同的James-Stein估计，也即共用一条直线），线的上端点对应着均值估计，下端点对应着James-Stein估计。可以看到Stein的估计方法就是将每个运动员的个人平均值向总平均进行收缩(Shrinking)。

Stein估计的理论基于一种断言：那就是不同运动员的真实击球能力的分布要比对应的初步均值估计的分布更加紧凑。收缩参数$\ c\ $就给出了这种矫正的幅度。

我们简单解释一下James-Stein估计中不同量的变化对收缩因子$\ c\ $的影响。首先我们先给出$\ c \ $的具体形式

$c=1-\frac{(k-3)\sigma^2}{\sum(y-\bar y)^2}$

首先我们先假定了不同运动员的真实击球能力分布事实上要更加紧凑，这意味着总体的方差较小，也即不同运动员的均值估计其实都在总平均附近。当$\ \sum(y-\bar y)^2\ $增加时，那么$\ c\ $增加，收缩程度降低，当$\ \sum(y-\bar y)^2\ $减少时，那么$\ c\ $减少，收缩程度增加。也就是说当数据支持预先的假定时，所有估计都会更加靠近总平均，但是如果数据不支持预先的假定时，那么收缩程度就会有所限制。

Stein估计似乎还存在着一种悖论的本质——不同地区、不同联盟的运动的击球水平竟然会相互影响？比如说我们知道了中国某个运动员的击球水平的初步估计（假如说他的能力比18位运动员中最差劲的ALVIS还要不堪），并且也将他的表现加入考虑时，最好的运动员CLEMENTE的估计也会随之受到影响。Stein估计似乎并不要求估计的对象各部分之间有着合乎情理的联系。

贝叶斯估计

我们尝试通过贝叶斯估计的角度导出James-Stein估计。

首先对$\ \mu\ $赋予一个均值为0，方差为$\ \sigma^2\ $的高斯先验分布，即$\ \mu_i\sim N(0,\sigma^2),1\le i\le m$；根据贝叶斯公式我们可以算出后验分布

$\pi(\mu_i|X)=N((1-\frac{1}{1+\sigma^2})x_i,\frac{\sigma^2}{1+\sigma^2})$

若取平方损失函数，$\mu_i\ $的贝叶斯估计正好对应其后验均值

$\delta^{\pi}(\mu)=(1-\frac{1}{1+\sigma^2})\mathbf{X}$

此时若取$\ \sigma^2=\frac{\mathbf{X}^T\mathbf{X}}{m-2}-1$，那么贝叶斯的估计就恰好等于James-Stein估计。

事实上，$\frac{\mathbf{X}^T\mathbf{X}}{m-2}-1\ $可以作为$\ \sigma^2\ $的估计，但不是UMVUE的。

收缩估计 Shrinkage

James-Stein估计是一种收缩估计，具体来讲就是将估计值向平均值移动，或在某些情况下向零收缩。James-Stein估计根据参数的方差对无偏估计$\ \mathbf{X}\ $进行了收缩，使得新的估计的均方误差更小。这种收缩的思想还体现在了Ridge-Regression和Lasso-Regression中。

一个估计的均方误差由方差和偏差的平方两部分组成，当存在复共线性性时，最小二乘估计虽然仍保持偏差部分为零，但它的平方却很大，最终致使它的均方误差很大。我们引入岭估计是以牺牲有偏性，换取方差部分的大幅减少，最终降低其均方误差。